링크 : https://www.acmicpc.net/problem/3830
문제 설명 :
상근이는 매일 아침 실험실로 출근해서 샘플의 무게를 재는 일을 하고 있다. 상근이는 두 샘플을 고른 뒤, 저울을 이용해서 무게의 차이를 잰다.
교수님의 마음에 들기 위해서 매일 아침부터 무게를 재고 있지만, 가끔 교수님이 실험실에 들어와서 상근이에게 어떤 두 샘플의 무게의 차이를 물어보기도 한다. 이때, 상근이는 지금까지 잰 결과를 바탕으로 대답을 할 수도 있고, 못 할 수도 있다.
상근이는 결과를 출근한 첫 날부터 공책에 적어 두었다. 하지만, 엄청난 양의 무게가 적혀있기 때문에, 교수님의 질문에 재빨리 대답할 수가 없었다. 이런 상근이를 위해서 프로그램을 만들려고 한다.
상근이가 실험실에서 한 일이 순서대로 주어진다. 어떤 두 샘플의 무게의 차이를 구할 수 있는지 없는지를 알아내는 프로그램을 작성하시오.
입력 :
입력은 여러 개의 테스트 케이스로 이루어져 있다.
각 테스트 케이스의 첫째 줄에는 샘플의 종류의 개수 N (2 ≤ N ≤ 100,000)과 상근이가 실험실에서 한 일의 수 M (1 ≤ M ≤ 100,000)이 주어진다. 샘플은 1번부터 N번까지 번호가 매겨져 있다. 다음 M개 줄에는 상근이가 실험실에서 한 일이 주어진다.
상근이가 무게를 쟀다면, ! a b w와 같은 형식으로 주어진다. 이 뜻은 b가 a보다 w그램 무겁다는 뜻이다. (a ≠ b) w는 1,000,000을 넘지 않는 음이 아닌 정수이다. 모든 측정은 정확하고, 일관성을 유지한다.
교수님의 질문은 ? a b와 같은 형식으로 주어진다. 이 뜻은 b가 a보다 얼마나 무거운지를 출력하라는 뜻이다.
마지막 줄에는 0이 두 개 주어진다.
출력 :
교수님의 질문 (? a b)이 입력으로 들어올 때 마다, 지금까지 측정한 결과를 바탕으로 a와 b의 무게 차이를 계산할 수 있다면, b가 a보다 얼마나 무거운지를 출력한다. 무게의 차이의 절댓값이 1,000,000을 넘지 않는다. 만약, 측정한 결과를 바탕으로 무게의 차이를 계산할 수 없다면, "UNKNOWN"을 출력한다.
예제 입력 :
2 2
! 1 2 1
? 1 2
2 2
! 1 2 1
? 2 1
4 7
! 1 2 100
? 2 3
! 2 3 100
? 2 3
? 1 3
! 4 3 150
? 4 1
0 0
예제 출력 :
1
-1
UNKNOWN
100
200
-50
접근법 :
1) 어떻게 풀 것인가?
N이 10만으로 적지 않은 편이고, 실시간으로 간선이 추가되며 샘플들의 관계가 변화한다.
샘플의 관계가 고정되어있다면 LCA로 간선간의 거리를 구하는데 용이할 것 같으나,
간선이 추가될 경우 재구성이 필요해 시간초과가 예상된다.
다시 문제로 돌아와 답을 구하려면 필요한 것은 2개이다.
① 2개 정점의 거리 차이를 측정할 수 있는가?
② 그 거리가 얼마인가?
①은 비교적 간단하다.
union find 를 사용한다면 2개 정점이 같은 그룹인지 확인하는 방식으로 구할 수 있다.
②의 경우 기존 union find를 활용해서 구할 수 있다.
예제를 그림으로 표현해보자.
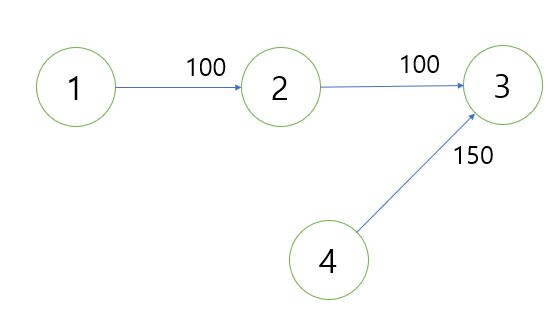
먼저 dist[ i ] 배열을 만들어 루트 노드와 i 와의 거리를 배열로 만든다고 했을때,
위 그래프에서 루트 노드가 3이라고 가정하면,
dist[ 1 ] = 200; parent[1] = 3;
dist[ 2 ] = 100; parent[1] = 3;
dist[ 3 ] = 0; parent[1] = 3;
dist[ 4 ] = 150; parent[1] = 3;
이라고 한다면, 1~4 같은 그룹내의 모든 노드간의 상대 거리를 구할 수 있다.
그러기위해 find 함수는
1. dist[ id ] 에 자신의 바로 앞선 dist[ parent[id] ] 를 더해주고,
2. return 을 할때 parent[ id ] 를 갱신시켜주면 된다.
static int find(int id) {
// 1. root인 경우 기존 union find 동일
if (parent[id] == id)
return id;
// 2. root가 아닌 경우 root와의 거리를 구해서 갱신
int pId = find(parent[id]);
dist[id] += dist[parent[id]];
return parent[id] = pId;
}
union 함수는 아래 그림을 코드로 구현하면 다음과 같다.

pa + dist[a] = a;
a + w = b;
b = pb + dist[b];
pa + dist[a] = b - w;
pa + dist[a] = pb + dist[b] - w;
pa + (dist[a] – dist[b] + w) = pb;
static void union(int a, int b, long diff) {
int pa = find(a);
int pb = find(b);
// 이미 같은 그룹이면 거리 계산이 되어있으므로 종료
if (pa == pb)
return;
// parent를 변경하고, 무게 차이를 갱신
dist[pb] = dist[a] - dist[b] + diff;
parent[pb] = pa;
return;
}
전체 코드는 아래 참조
2) 시간복잡도
유니온파인드의 일반적인 시간복잡도 O(logN)이라 가정하면 O(M logN) 이다.
테스트 케이스의 개수가 공개되어있지는 않으나 통과에는 무리가 없다.
(Java 기준 - 1,632ms)
3) 공간복잡도
M이 100만으로 크지 않아 고려하지 않음
4) 풀면서 놓쳤던점
특별히 없음.
5) 이 문제를 통해 얻어갈 것
유니온 파인드 활용법
Java 코드 :
import java.io.*;
import java.util.*;
// 3830 교수님은 기다리지 않는다
public class Main {
static int N, M;
static int[] parent;
static long[] dist;
static String type;
static int a, b, w;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb = new StringBuilder();
StringTokenizer st;
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
// N, M이 0, 0 이면 종료
for (; N != 0 && M != 0;) {
// Union Find를 위한 parent 초기화
parent = new int[N + 1];
for (int i = 1; i <= N; i++) {
parent[i] = i;
}
dist = new long[N + 1];
for (int i = 1; i <= M; i++) {
st = new StringTokenizer(br.readLine());
type = st.nextToken();
// 1. 무게를 쟀을 경우 - 판단 가능한 그룹으로 union
if (type.equals("!")) {
a = Integer.parseInt(st.nextToken());
b = Integer.parseInt(st.nextToken());
w = Integer.parseInt(st.nextToken());
union(a, b, w);
}
// 2. 무게를 판단하는 경우
else {
a = Integer.parseInt(st.nextToken());
b = Integer.parseInt(st.nextToken());
// 2-1. 무게를 판단할수 없는 경우 UNKNOWN
if (find(a) != find(b)) {
sb.append("UNKNOWN\n");
}
// 2-2. 무게를 판단할 수 있는 경우
else {
sb.append((dist[b] - dist[a]) + "\n");
}
}
}
// 다음 테스트 케이스의 N, M 입력받기
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
}
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
static int find(int id) {
// 1. root인 경우 기존 union find 동일
if (parent[id] == id)
return id;
// 2. root가 아닌 경우 root와의 거리를 구해서 갱신
int pId = find(parent[id]);
dist[id] += dist[parent[id]];
return parent[id] = pId;
}
static void union(int a, int b, long diff) {
int pa = find(a);
int pb = find(b);
// 이미 같은 그룹이면 거리 계산이 되어있으므로 종료
if (pa == pb)
return;
// parent를 변경하고, 무게 차이를 갱신
dist[pb] = dist[a] - dist[b] + diff;
parent[pb] = pa;
return;
}
}
+ Union Find를 몰랐을때 구현한
C 코드 :
// 3830 교수님은 기다리지 않는다 - 영준이의 무게측정 유사문제
#if 1
#pragma warning (disable : 4996)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int N, M;
struct st {
int value, flag;
};
int main(void)
{
register int i, j;
int tmp1, tmp2, judge, flag, tmp_flag, tmp_value;
char tmp;
struct st *p;
flag = 1;
for (; ; )
{
scanf("%d %d", &N, &M);
if (!N) break;
p = (struct st *) calloc(N+2, sizeof(struct st));
for (i = 1; i <= M; i++)
{
scanf(" %c", &tmp);
if (tmp == '!')
{
scanf("%d %d %d", &tmp1, &tmp2, &judge);
if (p[tmp1].flag == 0 && p[tmp2].flag == 0)
{
p[tmp1].value = p[tmp1].flag = p[tmp2].flag = flag;
p[tmp2].value = flag + judge;
flag++;
}
else if (p[tmp1].flag && !p[tmp2].flag)
{
p[tmp2].value = p[tmp1].value + judge;
p[tmp2].flag = p[tmp1].flag;
}
else if (p[tmp2].flag && !p[tmp1].flag)
{
p[tmp1].value = p[tmp2].value - judge;
p[tmp1].flag = p[tmp2].flag;
}
else if (p[tmp1].flag == p[tmp2].flag) continue;
else
{
tmp_flag = p[tmp2].flag;
tmp_value = p[tmp2].value;
p[tmp2].value = p[tmp1].value + judge;
p[tmp2].flag = p[tmp1].flag;
for (j = 1; j <= N; j++)
{
if (p[j].flag == tmp_flag)
{
p[j].value = p[j].value - tmp_value + p[tmp2].value;
p[j].flag = p[tmp2].flag;
}
}
}
}
else
{
scanf("%d %d", &tmp1, &tmp2);
if (p[tmp1].flag == p[tmp2].flag && p[tmp1].flag)
{
printf("%d\n", p[tmp2].value - p[tmp1].value);
}
else printf("UNKNOWN\n");
}
}
}
return 0;
}
#endif
'알고리즘 Algorithm > BOJ 백준 (초급~중급)' 카테고리의 다른 글
| [BOJ 백준] 도로 네트워크(3176) Java (0) | 2021.07.26 |
|---|---|
| [BOJ 백준] LCA 2(11438) Java (0) | 2021.07.26 |
| [BOJ 백준] 단절점(11266) Java (0) | 2021.07.25 |
| [BOJ 백준] 정수 삼각형(1932) Java (0) | 2021.07.22 |
| [BOJ 백준] 플로이드(11404) Java (0) | 2021.07.22 |



